Mixture of Experts LLM (MoE)
요즘 핫한 MoE 에 대해 알아보자.
MoE가 왜 필요한가?
Transformers 구조에서 메모리와 시간복잡도 모두 Attention 구조의 착안하여 증가한다. 그렇기 때문에 LLM에서 Self Attention 이 연산에서 큰 부분을 차지한다고 생각하기 쉽다. 하지만 실제 파라미터 수가 더 많고 연산에 꽤 많은 부분을 차지하는것은 Feed Forward Network 부분이다.
LLama2-13B 의 LlamaDecoderLayer은 Self Attention 과 MLP (Feed Forward) 두개로 나누어져 있고 각각 파라미터 수를 계산하면 다음과 같다.
| LLama2-13B | LlamaAttention | LlamaMLP |
|---|---|---|
| 13.02B | 4.19B | 8.49B |
이와 같이 Llama 에서 MLP 가 Attention의 모든 query,key,value 파라미터 보다도 2배 가까이 많은것을 알 수 있다.
즉, Attention 보다도 Feed Foward 레이어를 최적화하는것이 전체적인 throughput 향상에 도움이 될 수 있다.
Mixtral 8x7B
그렇다면, MoE 로 핫한 Mistral 은 어떤가? Mistral 8x7B 도 똑같이 구해보자.
| Mistral 8x7B | MixtralAttention | MixtralMoeBlock |
|---|---|---|
| 46.70B | 1.34B | 45.10B |
Mistral 의 경우 MixtralMoeBlock 의 8개의 Experts 가 파라미터가 MistralAttention 보다 무려 33배가 많다. 실제 여기서 2개의 Expert 를 사용하니 Inference 자체에 사용되는 양은 $33/4 \approx 8$ 배 정도일것이다.
물론 Mixtral 8x7B 는 조금 다른 방식의 Scaling 을 쓰고있다.
우선, Scaling Laws for Neural Language Models 논문의 e.q:2.1 을 보면,
\[d_{\text{attn}} = d_{\text{ff}}/4 = d_{\text{model}}\]위 와 같이 Feed Foward 의 중간 차원 $d_{\text{ff}}$ 은 전체 모델 및 Attention 의 차원 $d_{\text{attn}}, d_{\text{model}}$ 에 1/4 가 되게 설정한 채로 Scaling 을 진행한다.
Llama2 와 Mixtral 8x7B의 $d_{\text{ff}}/d_{\text{model}}$ 를 계산해보자.
| Model | $d_{\text{ff}}$ | $d_{\text{model}}$ | $d_{\text{ff}}/d_{\text{model}}$ |
|---|---|---|---|
| Kaplan et al. | - | - | 4 |
| Llama2 13B | 13824 | 5120 | 2.7 |
| Mixtral 8x7B | 14336 | 4096 | 3.5 |
하지만 Mixtral 의 경우 Query 와 Key Projection 의 Output 차원이 다르므로 Query Output Dimension 을 기준으로 계산하였다. 결과적으로는 Mixtral 도 $d_{\text{ff}}/d_{\text{model}}$ 가 3.5 로 4보다 작다.
Llama2와 확연히 다른점은 Attention 쪽 파라미터가 더 작으면서 (Llama2-13B는 4.19B, Mixtral 8x7B 은 1.34B) Feed Forward 의 $d_{\text{ff}}$ 를 Scaling 한 것이다. 이러한 구조를 통해 Llama2 보다 더 좋은 성능을 낸다고 리포트하고 있다.
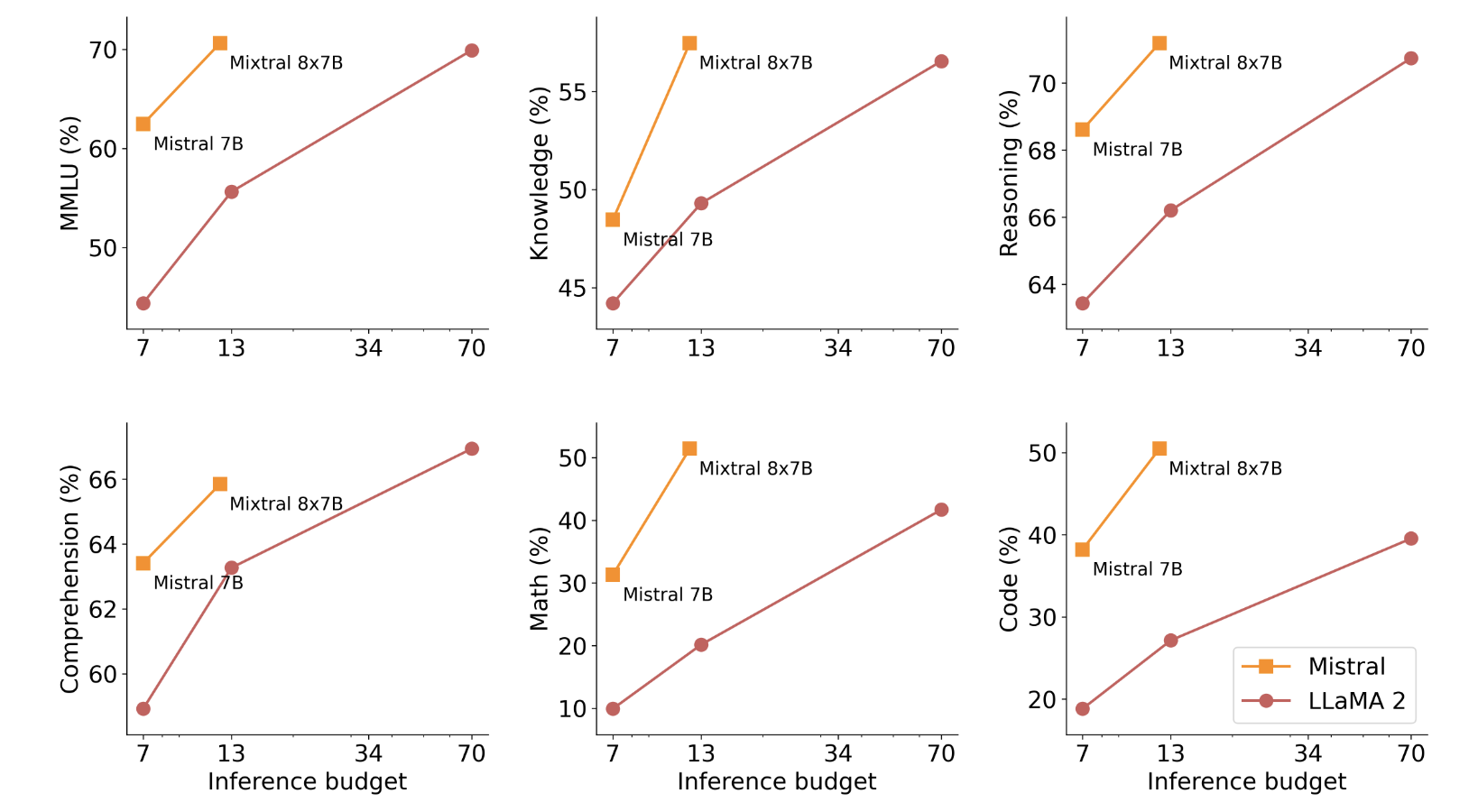
이 Figure 가 가장 전반적인 성능을 볼 수 있는 것 같아 가지고 왔다. Mixtral 8x7B는 Active Paramater 가 12B (실제 2개의 Experts만 선택을 하니까) 인데 대충 Llama13B와 비교해도 성능이 높고 70B보다도 좋다는것을 강조하고 싶었던것 같다.
Mixtral 8x7B가 전체 Param 이 46B 정도인데 70B Llama2 보다 Code, Math 같이 Reasoning 이 많이 필요한 곳에서도 월등히 잘하는것은 결과에 조금 의구심이 들기도한다. 물론 CodeLlama 가 Code 부분에서 더 잘하는것을 생각해보면 벤치마킹을 위해 데이터셋을 보강하고 집중적으로 훈련시키면 불가능한 부분은 아니라는 생각이 들긴한다.
몇가지 더 궁금한 점은
- 우선, 모든 Experts 를 다 쓰도록 Inference 하면 성능이 더 떨어지는지
- Knowledge, MATH, Code … 각기 다른 벤치마크에서 MoE의 특정 Experts 가 계속 선택이 되는지가 조금 궁금하다.
그런데 그런 실험 결과를 리포트하지 않은것을 보면 어쩌면 Experts 를 다 쓰게하면 성능이 떨어지는것이 아닐까 싶다. 혹시나 해서 🤗HF 의 discussions 를 찾아보았는데 Experts 를 다 쓰는 경우에 대한 성능리포트를 대신 해준 사람은 없는것 같다.
Routing Analysis
Mixtral of Experts 라는 제목으로 논문이 공개가 되었고 위의 두번째 질문 (“Knowledge, MATH, Code 등 각기 다른 벤치마크에서 MoE의 특정 Experts 가 계속 선택이 되는지가 조금 궁금하다. “) 에 대해서 Routing Analysis 에서 분석하고 있어 관련 내용을 정리해보았다.
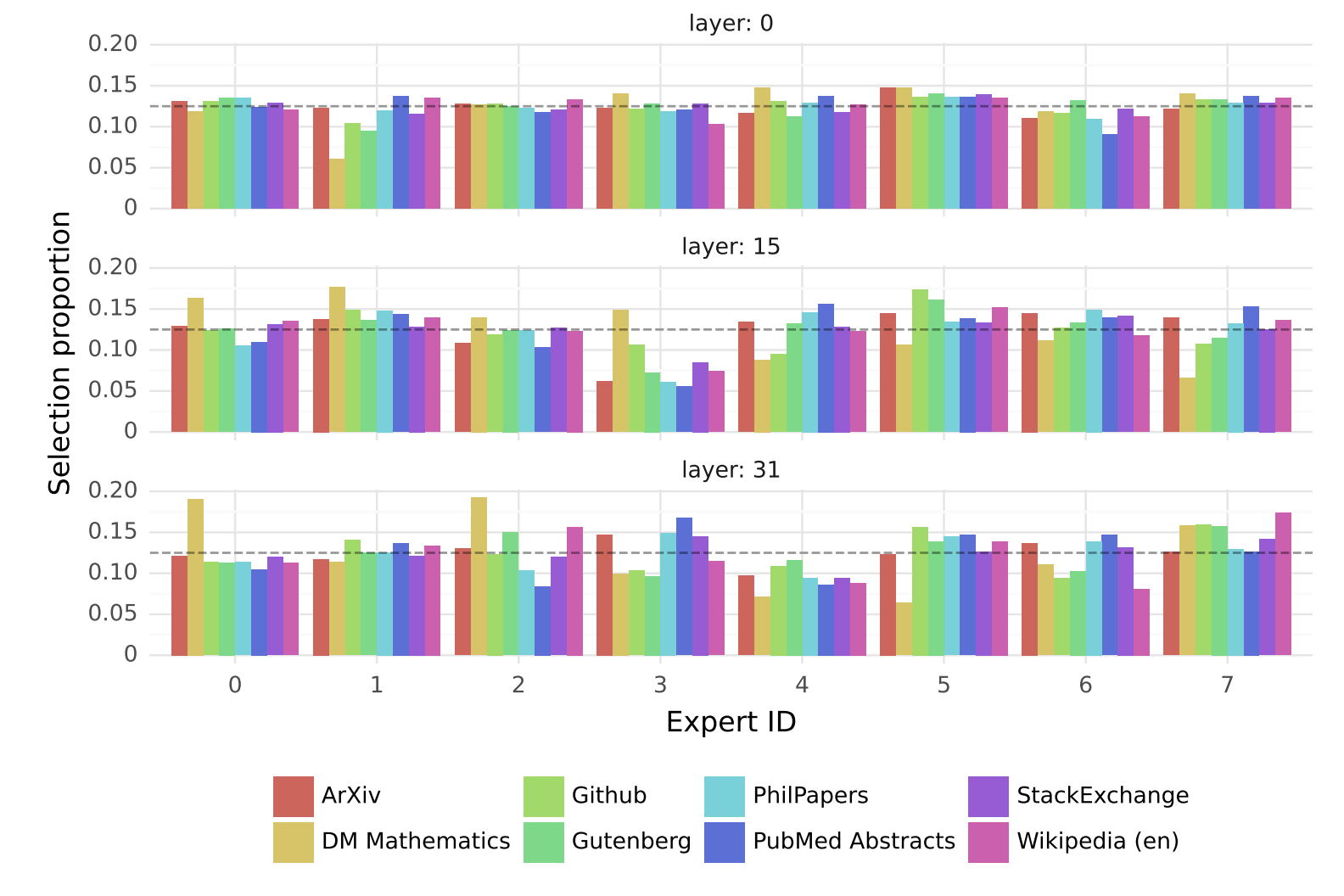
Pile 데이터셋에서 전체 시퀀스를 넣고 각각 도메인 (Arxiv, Github 등등) 에서 각각 Experts 들이 얼마나 Selection 되는지를 정리한 도식이다. 회색 dash line 이 1/8 이어서 이 회색선 위에 위치한것은 그만큼 많이 선택된 Experts 라는 것이다. 수학($\texttt{DM Mathematics}$) 는 31번째 Layer 에서 압도적으로 0번 Expert 에 의해 선택된것을 확인해볼 수 있다. 반대로 똑같이 31번째 Layer 에서 언어가 좀더 많은 데이터셋인 $\texttt{StackExchange},\texttt{Wikipedia}$ 에서는 8번째 Expert가 선택된것도 재밌다. 또 0번째 Layer 에서는 비교적 균등하게 선택되다가 Layer 가 점점더 깊이 올라올 수록 특정 도메인에 특정 Expert 가 더 많이 선택되는 결과도 재밌다.